Оригинал: Srivastava, Hinton, Krizhevsky, Sutskever and Salakhutdinov, Dropout: A Simple Way to Prevent Neural Networks from Overfitting // Journal of Machine Learning Research 15 (2014) 1929-1958
Ключевые слова: нейронные сети, регуляризация, комбинированные модели, глубокое обучение
Введение
Глубокие нейронные сети содержат множество нелинейных скрытых слоев, что делает их очень точными моделями, которые могут аппроксимировать очень сложные отношения между своими входами и выходами. При ограниченном наборе обучающих данных, многие из этих сложных отношений будет являться результатом шума выборки, так как они будут только в обучающей выборке, а не в реальных тестовых данных, даже если они взяты из одного распределения. Это приводит к чрезмерной настройке коэффициентов и привело к разработке множества методов для уменьшения этого эффекта. Эти методы включают в себя прекращение обучения, как только производительность на проверочном множестве становится хуже, вводя различные виды весов “наказания”, таких как L1 и L2 регуляризация и обмена мягкими коэффициентами (Nowlan and Hinton, 1992).Без ограничения на количества вычислений, лучший способ "регуляризации" модели фиксированного размера является усреднение предсказаний всех возможных настроек параметров, взвешивания каждого параметра по его апостериорной вероятности обучающих данных. Иногда это может быть достаточно хорошо аппроксимировано для простых и/или небольших моделей (Xiong et al., 2011; Salakhutdinov and Mnih, 2008), однако желательно приблизиться к качеству байесовского золотого стандарта с использованием значительно меньшего количества вычислений. В статье предлагается сделать это путем аппроксимации равновзвешенных средних геометрических средних значений экспоненциального числа изученных моделей с общими параметрами.
Рисунок 1. — Прореживание нейронной сети. Слева — обычная нейронная сеть с двумя скрытыми слоями. Справа — пример прореженной нейронной сети представленной слева.
Комбинация моделей почти всегда улучшает производительность методов машинного обучения. Однако, при наличии больших нейронных сетей, очевидно, что идея усреднения результатов многих отдельно обученных сетей непозволительно дорога. Объединение нескольких моделей является наиболее полезным, когда отдельные модели отличаются друг от друга, и для того, чтобы нейронные сети моделей различали их, то они должны либо иметь различные архитектуры, либо обучаться по разным данным. Обучение множества различных архитектур трудозатрано, так как поиск оптимальных гиперпараметров для каждой архитектуры является сложной задачей и обучение каждой большой сети требует множества вычислений. Кроме того, большие сети обычно требуют большого количества обучающих данных и могут быть недоступны для обучения разных сетей на разных подмножествах данных. Даже если имеется возможность обучения нескольких различных больших сетей, использование их все время проведения испытания является недопустимым в приложениях, где важно время реакции.
“Dropout” является методом, который решает обе эти проблемы. Это предотвращает переобучение и обеспечивает способ объединения приблизительно экспоненциального количества различных сетевых архитектур нейронных сетей. Термин "Dropout" относится к отключению блоков (скрытых или видимых) в нейронной сети. Под отключением блоков имеется в виду временное удаление их из сети, вместе со всеми входящими и исходящими соединениями, как показано на рисунке 1. Выбор, элементов для удаления является случайным. В простейшем случае, каждый блок учитывается в сети с фиксированной вероятностью р независимо от других единиц, где р может быть выбрано с помощью проверочного набора или может просто быть установлен на уровне 0,5, который, близок к оптимальной для широкого диапазона сетей и заданий. Для входных блоков, тем не менее, оптимальная вероятность удержания, как правило, ближе к 1, чем 0,5.
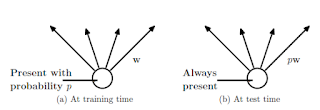
Рисунок 2 — Слева нейрон имеет вероятность сохранения p, Справа — во время тестирования выходы нейрона умножатся на p.
Разрежение нейронной сети приводит к выборке "сокращенных" сетей из нее. Сокращенная сеть состоит из всех единиц, которые прошли отсев (рис 1b). Нейронную сеть из n блоков, можно рассматривать как совокупность 2^n возможных сокращенных нейронных сетей. Все сети имеют общие веса, таким образом общее число параметров по-прежнему O(n^2) или меньше. Для каждого представления обучающих наборов данных, новая сокращенная сеть оцифровывается и обучается. Таким образом, обучение нейронной сети с отсевом можно рассматривать как обучение коллекцию 2^n разреженных сетей с широким распределением весов, где каждая разреженная сеть обучается редко, если вообще обучается.
Во время тестирования не представляется возможным явно усреднить предсказания с экспоненциального числа сокращенных сетей. Тем не менее, есть очень простой приближенный метод усреднения хорошо работает на практике. Идея заключается в том, чтобы использовать одну нейронную сеть во время испытания без сокращения. Веса этой сети являются предварительной версией обученных весов. Если блок сохраняется с вероятностью р во время тренировки, исходящие веса этой единицы умножается на р во время теста, как показано на рисунке 2. Это гарантирует, что для любого скрытого блока ожидаемый выход такой же, как фактический выход во время испытания. Делая это масштабирование, 2^ n сетей с общими весами могут быть объединены в единую нейронную сеть для использования во время испытания. Мы обнаружили, что обучение сети с использованием разрежения и этот приближенный метод усреднения по времени тестирования приводит к значительно более низкой ошибке обобщения на самых разнообразных задачах классификации по сравнению с обучением другими методами регуляризации.
Идея разрежения не ограничивается нейронной сети с прямым распространением сигнала. В более общем случае применимо к графическим моделям, таких как больцмановские машины. В этой статье мы рассматриваем разряженную модель ограниченной больцмановской машины в сравнении его со стандартной ограниченной больцмановской машиной (RBM). Наши эксперименты показывают, что в некоторых случаях разряженные RBM лучше, чем стандартные RBM.
Эта статья структурирована следующим образом. Раздел 2 описывает мотивацию к этой идее. Раздел 3 описывает соответствующую предыдущую работу. Раздел 4 формально описывает модель разрежения. В разделе 5 дается алгоритм обучения разреженных сетей. В разделе 6 мы представляем наши экспериментальные результаты, где мы применяем разрежение к задачам в различных областях и сравниваем их с другими методами регуляризации и комбинирования моделей. В разделе 7 анализируется влияние отсева на различные свойства нейронной сети и описывается, как недообученность взаимодействует с гиперпараметрами сети. Раздел 8 описывает модель разряженных RBM. В разделе 9 мы исследуем идею промежуточного разрежения. В приложении А представлено практическое руководство по обучению разреженных сетей. Оно включает в себя подробный анализ практических соображений, в выборе гиперпараметров при обучении сетей.
Продолжение следует...


LuckyClub Casino Site - Live Dealers, Bonuses and Games
ОтветитьУдалитьLucky Club Casino Site. It's a luckyclub reliable online casino and the choice of many experienced players is the one thing that many people overlook.